1) Sens de Variation
Soit une fonction f définie et dérivable sur un intervalle I.
La pression est une notion physique fondamentale. Elle correspond à la force par unité de surface qu’exerce un fluide ou un solide sur celle-ci. Il s’agit d’une grandeur scalaire dont l’unité dans le système international d’unités (SI) est le pascal (Pa), lequel correspond à une force de un newton (N) par mètre carré (m2) .
DEFINITION: La masse volumique d’une substance est la masse d’une unité de volume de cette substance.
Elle est généralement notée par les lettres grecques ρ (rhô) ou µ (mu).
Elle s’exprime en g/cm3 ou kg/m3.
Exercice 1:
a) Soit (Vn)n≥0 une suite telle que V0 = 2 et Vn+1 = 3Vn−2. La suite est-elle arithmétique? Géométrique?
b) Soit (Un)n≥0 définie par Un = Vn−1. Démontrer que (Un)n≥0 est une suite géométrique.
c) Exprimer Un en fonction de n.
d) En déduire Vn en fonction de n.
e) Calculer V100 .
Solution:
a) Une suite arithmétique est une suite de nombres que l’on obtient en ajoutant une constante (raison : r) au précédent.
D’une manière générale, une suite (Un) est arithmétique de premier terme U0 et de raison r, si pour tout n, Un+1=Un+r
Pour démontrer qu’une suite est arithmétique, nous avons deux possibilités :
La courbe représentative de la fonction trinôme f(x) = ax2+bx+c, dans le repère orthogonal s’appelle parabole.
Certains points jouent un rôle particulier:
1) Les points d’intersection de la courbe Cf avec l’axe (Ox):
Soit une parabole Cf de la fonction f(x) = ax2+bx+c .
Rappel: Tous les points de (Ox) ont pour ordonnée 0.
……
……
1) 2001 / İKİNCİ AŞAMA / DEUXIÈME ÉTAPE
ORTAK DERSLER / TRONC COMMUN
Une fonction f vérifie: f(x) – f(x+3) = x+2.
Déterminer f(2) sachant que f(8) = 8
a) 20 b) 17 c) 19 d) 18 e) 24
SOLUTION:
Pour x = 2, on a: f(2) – f(5) = 4
Pour x = 5, on a: f(5) – f(8) = 7
f(2) – f(8) = 11 => f(2) – 8 = 11 => f(2) = 19
Réponse: C
…
Soit P un polynôme. Le reste de la division de P par x-2 est 9, le reste de la division de P par x+1 est -3. Quel est le reste de la division de P par (x-2).(x+1)?
a) -27 b) -3 c) 4x-1 d) 4x+1 e) 0
SOLUTION: Le reste de la division de P par x-2 est 9 => P(2) = 9 (1)
(2 est la racine de x-2)
Le reste de la division de P par x+1 est -3 => P(-1) = -3 (2)
(-1 est la racine de x+1)
…
DEFINITIONS
L
a masse molaire d’un composé moléculaire se calcule en additionnant les masses molaires de tous les éléments qui constituent ses molécules partie en les multipliant par les coefficients de la formule brute de ce composé.
Son symbole est M.
…
LE THERMOMETRE
.
La chaleur (Isı): La chaleur est une forme d’énergie. Les matières sont faites à partir des atomes. L’énergie de la chaleur est reliée au movement de ces atomes.
Isı, bir enerji biçimidir ve maddeyi oluşturan küçük parçaların, yani atomların hareket enerjileriyle ilgilidir.
Konumuzu işlerken ısının bir enerji çeşidi olduğunu unutmamalıyız. Bu durumda ısı birimleri
Calorie (cal) ve Joule (J)
olarak alınacaktır. Bunlardan hangisini kullanacağımıza soruda verilenlerin birimlerine bakarak ya da sorunun bizden hangi birimde istediğine dikkat ederek karar veririz.
La température (sıcaklık): La température est un indice de la vitesse des particules. Un thermomètre est un instrument de mesure des températures.
Sıcaklık, maddeyi olusturan parçacıkların hızının bir göstergesidir ve termometreler, sıcaklığı ölçerken kullandığımız araçlardır.
Konumuz içinde ilk olarak sıcaklık (température) ile ilgili işlemler yapacağız.
Sıcaklık (température) ölçmek için kullandığımız farklı türde ölçüler vardır. Göreceğimiz bu farklı ölçme biçimlerinde ortak olan nokta şudur: Her birinde suyun donma noktası (la température de solidification de l’eau) ve suyun kaynama noktası (la température d’ébullition de l’eau) için önerilen belli sıcaklıklar vardır. Bunlar arasındaki ilişkiyi anlayabilirsek soruları çözerken daha rahat ederiz ve formülleri unutsak bile kendimiz farklı ölçüler arasında çevirmeleri rahatlıkla yapabiliriz.
.
Burada özellikle Dame de Sion ve St. Pulcherie öğrencileri için bir uyarıda bulunmak isterim: Kitaplarınızda ya da size dağıtılan ders notlarında (fotokopilerde) Réaumur yanlış yazılmış (Réamur olarak) olabilir. Bu sıcaklık ölçüm sistemini ortaya koyan bilim adamı René-Antoine Ferchault de Réaumur (1683-1757)’dür. Yani doğrusu bizim yazdığımız gibidir.
.
| chaleur_temp_1 | Celsius (centigrade) | Fahrenheit | Kelvin | Réaumur |
| Point de solidification de l’eau | 0 | 32 | 273 | 0 |
| Point d’ébullition de l’eau | 100 | 212 | 373 | 80 |
.
Bu termometre ölçeklerinin birbirlerine nasıl çevrildiklerini örneklerle açıklayalım:
.
Exemple 1.
Exprimer en degrés Réaumur et en degrés Fahrenheit les températures suivantes:
80°C; 120°C; 10°C
Bu dönüşümleri yapmak için doğru orantı kurmayı bilmek yeterlidir (konunun ilerleyen bölümlerinde gerekli formüller de verilecektir).
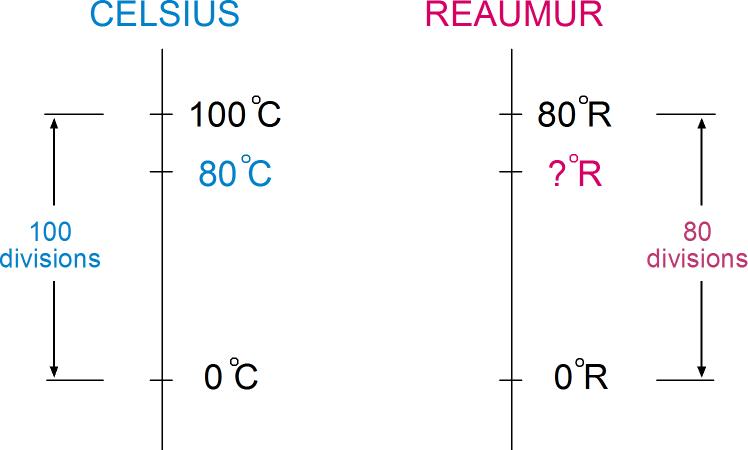
Réaumur’de, suyun donma noktası 0°R, kaynama noktası 80°R olarak alınır.
Celsius’ta ise bildiğimiz gibi suyun donma noktası 0°C, kaynama noktası 100°C’dir.
.
.
Şekilden de anlaşılabileceği gibi bu iki termometrede suyun donma noktası ile kaynama noktası arası farklı sayıda bölmeye (division) ayrılmıştır. Sorumuzu basit bir orantıyla çözebiliriz. Celsius ölçeği kullanan termometrede sıcaklık göstergesi 100 bölmede 80 bölme yükselmektedir. Acaba bu, 80 bölmede (yani Réaumur kullanıldığında) kaç bölmeye denk gelmektedir?
.
.
Bu bir doğru orantı olduğundan içlerle dışların çarpımı eşittir. Yani:
.
100 . X = 80 . 80
X = 6400 / 100 = 64 divisions
.
Demek ki Celsius’ta 80 bölme (divisions) Réaumur’de 64 bölmeye (divisions) denk geliyor.
Réaumur’un başlangıcı da 0° olduğundan herhangi bir ekleme ya da çıkarma yapmaya gerek yoktur. Buradan varacağımız sonuç:
.
80°C = 64°R
.
Orantımızdan görüldüğü gibi Celsius’u Réaumur’e çevirirken 80’le çarpıp 100’e böldük. Yani 80/100 ile, sadeleştirirsek 4/5 ile, ondalık (décimal) yazarsak 0,8’le çarptık.
Bunu formül olarak gösterirsek:
.
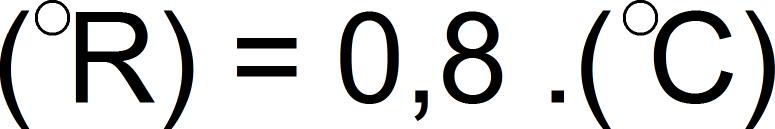
ya da
şeklinde yazabiliriz.
.
.
Buradan
.
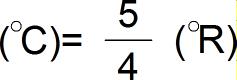
bulunabilir.
.
Aynı örnekten yola çıkarak 64°R’yi °C’ye çevirirsek:
.
.
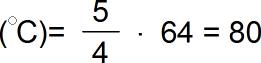
bulunur. Yani 64°R = 80°C ‘dir.
.
Sorunun çözümüne devam edersek…
120°C => 120 . 0,8 = 96°R ve 10°C => 10 . 0,8 = 8°R bulunur.
.
Şimdi de aynı sıcaklıkları Fahrenheit’a çevirelim. Aynı şekilde orantı kurabiliriz, ancak dikkat etmemiz gereken nokta, Fahrenheit’ta suyun donma noktası (32°F) ve kaynama noktası (212°F) arasının
212 – 32 = 180 bölme (divisions) olduğudur.
.
.
Bu bir doğru orantı olduğundan içlerle dışların çarpımı eşittir. Yani:
100 . X = 80 . 180
X = (80 . 180) / 100 = 144 divisions
.
Sonucu hemen 144 diye yazamayız, çünkü Fahrenheit, 32°’den başlar, yani bu 32 derecenin üzerine 144 bölme eklemeliyiz.
.
144 + 32 = 176 olduğundan 80°C = 176°F
yazılır ve sonuç bulunmuş olur.
.
Burada yaptığmız işlemleri de formüle dökmeye çalışalım. Öncelikle orantıyı kullandık. °C olarak verilen sıcaklığı (température) önce 180’le çarpıp, sonra 100’e böldük. Yani 180/100’le çarpmış olduk. Bu kesri sadeleştirerek 9/5 diye yazabiliriz. Ondalık (décimal) yazmak istersek kesrin 1,8’e eşit olduğunu bulabiliriz. Bu çarpmadan sonra, °C 0’dan, °F ise 32’den başladığı için bulduğumuz sonuca 32 ekledik.
Öyleyse:
.
.
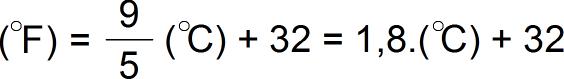
olarak yazılabilir.
Böylece:
120°C => 120 . (9/5) + 32 = 248°F ve 10°C => 10 . (9/5) + 32 = 50°F bulunur.
.
Fahrenheit’ı Celsius’a çevirmek istediğimizde ise önce (32 dereceden başladığı için) verilen sıcaklık değerinden 32 çıkarıp, sonra da 5/9’la çarpmak yeterli olacaktır.
Örneğin: 50°F => (50-32).(5/9) = 18.(5/9) = 10°C bulunur. Zaten bu sonucu yukarıda 10°C’yi Fahrenheit’a çevirirken bulmuştuk.
.
Celsius’u Kelvin’e çevirmek istediğimizde işimiz nispeten daha kolay olacaktır. Çünkü Kelvin suyun donma noktasını (la température solidification de l’eau) 273° ve suyun kaynama noktasını (la température de d’ébullition de l’eau) 373° olarak aldığından, bu aralığı 373-273=100 bölmeye ayırmış olur. Celsius’ta da bu aralık 100 bölme olduğundan, Kelvin’deki bir derecelik artış Celsius’ta da tam bir derecelik artışa denk gelir. Yalnızca, Kelvin 273’ten, Celcius ise 0’dan başladığından, Celsius Kelvin’e çevrilirken 273 eklemek gerekir.
.
Örneğin: 80°C => 80+273 = 353°K ’dir.
10°C = 10+273 = 283°K ve 120°C = 120+273 = 393°K olarak bulunur.
Tersini uygularsak, Celsius Kelvin’e çevrilirken verilen sıcaklıktan 273 çıkarmak yeterli olacaktır.
Örneğin: 330°K => 330 – 273 = 57°C şeklinde bulunabilir.
.
Exemple 2. Examiner le tableau suivant…. (Bu değerleri kendiniz çevirerek kontrol edin).
.
| -30°C | 243°K | -24°R | -22°F |
| -10°C | 263°K | -8°R | 14°F |
| 0°C | 273°K | 0°R | 32°F |
| 20°C | 293°K | 16°R | 68°F |
| 100°C | 373°K | 80°R | 212°F |
.
L’échelle X
Sorularımızda bazen de bu termometrelerin dışında, kendi ölçeklendirdiğimiz bir termometrede okunan sıcaklığın bilinen ölçeklere çevrilmesi istenebilir.
.
Exemple 3.
Gökçe veut fabriquer son propre thermomètre. Il fixe une échelle de température en choisissant -10° la température de solidification (température de fusion) de l’eau et 120° la température d’ébullition de l’eau. Gökçe obtient une mesure de 68 ºG sur son thermomètre. Quelle est la mesure correspondante sur l’échelle Celsius?
Bu sorumuzda meraklı bir arkadaşımız olan Gökçe, kendi termometresini yapmak istiyor. Bunu yaparken de suyun donma noktasını -10°G ve kaynama noktasını 120°G olarak işaretliyor. Sonra da bu termometrede 68°G’lik bir değer okuyor. Soru da bizden, bunun Celsius’ta kaç dereceye denk geldiğini bulmamızı istiyor. Bulalım:
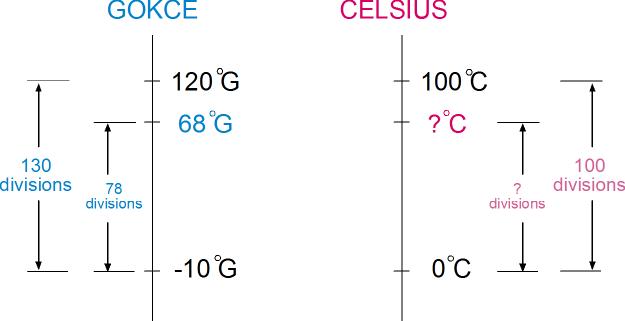
Bu sorularda da daha önce olduğu gibi basit bir orantı kurabiliriz. Gökçe’nin termometresinde suyun donma ve kaynama noktaları arasında kaç bölme (division) olduğunu bulalım.
.
.
Gökçe’nin termometresinde -10°G ile 120°G arasında 120-(-10) = 130 bölme (divisions) var
Bu 130 bölmede, 68-(-10) = 78 bölmelik bir yükselme olmuş.
Orantımızı kurarsak:
.
.
Bu bir doğru orantı olduğundan içlerle dışların çarpımı eşittir. Yani:
130 . X = 78 . 100
X = (78 . 100) / 130 = 60 divisions.
.
Celsius, 0°’den başladığına göre herhangi bir ekleme yapmaya gerek yoktur. Çünkü bu 60 bölme 0’ın üzerine eklenecektir.
.
Böylece: 78°G = 60°C bulmuş oluruz.
.
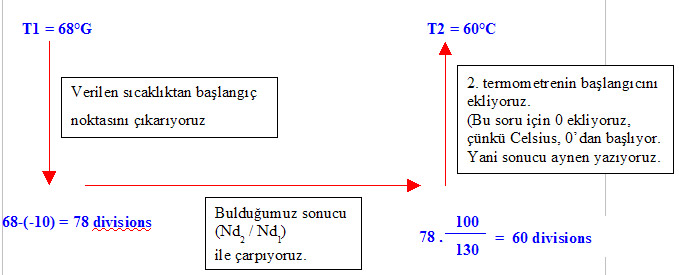
Bu sorunun çözümümünde şöyle bir yol gösteren öğretmenlerimiz de mevcuttur (Burda da aslında bizim izlediğimiz işlem sırası izlenmektedir):
Nd1: Nombre de divisions du premier thermomètre = 120-(-10) = 130 divisions
Nd2: Nombre de divisions du deuxième thermomètre = 100 division
.
Ders sonunda hatırlatmalar:
Isı (chaleur) ve sıcaklık (température) farklı kavramlardır, birbirine karıştırılmamalıdır.
“Point de solidification de l’eau”, “point de fusion de l’eau” aynı şeylerdir. Birincisi “suyun donma (katılaşma) noktası, ikincisi “suyun erime noktası” demektir. Erime noktasından bahsettiğimiz ve suyun katı hali buz olduğu için çeşitli kaynaklarda “point de fusion de la glace” olarak da karşımız çıkar. Ayrıca “point” (nokta) yerine “température” (sıcaklık) de denir: température de solidification de l’eau, température de fusion de l’eau, température d’ébullition de l’eau … gibi.
Peki bunu bilmek ne işimize yarar? Özellikle internet üzerindeki aramalarınızda bu sözcüklerle farklı farklı aramalar yaparsanız işinize daha çok yarayacak kaynaklara daha kısa sürede erişebilirsiniz. Bunlardan yalnızca birini kullanan bir kaynağı gözden kaçırmamış olursunuz.
Konu anlatımında “Celsius 0°’den başlıyor, Kelvin 273°’den başlıyor” gibi ifadeler kullandık. Aslında bu ifadeler yanlıştır, tabii ki örneğin Celsius’ta -5°C de ölçülebilir. Başlangıçtan kastımız, suyun donma noktasıdır. Biz, konunun daha rahat anlaşılabilmesi için böyle bir ifade kullandık.
Peki, negatif sıcaklıkların çevriminde bir değişiklik var mıdır? Hayır, yoktur..
Örneğin: -20°C => (-20) . 1,8 + 32 = -36 + 32 = -4°F şeklinde hesaplanabilir.
Yani 0°C’nin altında 20 bölme, Fahrenheit’ta 36 bölmeye denk gelir. Ancak Fahrenheit’ta suyun donma noktası 32°F alındığından, 32’den aşağıya doğru 36 bölme ineriz. Sonuç olarak 32 bölme sonra 0°F’ye, üzerine 4 bölme daha indiğimizde -4°F’ye ulaşmış oluruz (toplamda 36 bölme inmiş olduk)…
.
Bu dersin sonu….
1975 yılında Büyükada’da doğan Gökçe Doğan, ilk ve orta öğrenimini İznik’te tamamladıktan sonra, 1989 yılında Eskişehir Fatih Fen Lisesi’ni kazandı.
1992 yılında Mimar Sinan Üniversitesi’nde mimarlık eğitimine başladı, ancak bu bölümde aradığını bulamadı ve bu eğitimi yarıda bıraktı.
1994 yılında öğrenim görmeye başladığı Galatasaray Üniversitesi’nden 2001 yılında mezun oldu. Halen aynı üniversitede yüksek lisans tezini yazma aşamasındadır.
Üniversiteye başladığı 1992 yılından beri çesitli seviyelerdeki öğrencilerle çalışmalar yapan Gökçe Doğan, Galatasaray Üniversitesi’nde Fransızca öğrenmesinin ardından özellikle İstanbul’daki Fransız liselerinden öğrencilere matematik, fizik, kimya, geometri ve analitik geometri derslerini çalıştırmaya başlamış, bunun yanı sıra Türkçe derslerinde de öğrencilerine yardımcı olmuştur.
Sadece lise seviyesindeki öğrencilerle değil, daha küçük sınıflarla da çalışmalar yapmakta, bunun yanında SBS ve ÖSS’ye hazırlık dersleri vermekte, Fransız okullarındaki öğrenciler için Galatasaray Üniversitesi tarafından düzenlenen iç sınav için de bir hazırlık programı uygulamaktadır.
Ayrıca özellikle üniversitelerin ilk iki sınıfındaki öğrencilerle fizik, kimya ve “calculus” çalışmaktadır.
Bugüne kadar Saint Benoit, Saint Joseph, Sainte Pulcherie, Notre Dame de Sion, Pierre Loti gibi Fransız liseleri ve ENKA, Eyüboğlu Koleji, Özel Işık Lisesi, Tevfik Fikret Lisesi gibi özel okullardan öğrencilerle çalışmıştır. Bunlara ek olarak özellikle matematik ve fizik derslerinde Sabancı Üniversitesi’nden öğrencilere de yardımcı olmaktadır.